Gallery of featured posts

Deep Learning and Scientific Computing with R torch: the book
Please allow us to introduce Deep Learning and Scientific Computing with R torch. Released in e-book format today, and available freely online, this book starts out by introducing torch basics. From there, it moves on to various deep-learning use cases. Finally, it shows how to use torch for more general topics, such as matrix computations and the Fourier Transform.

Upside down, a cat's still a cat: Evolving image recognition with Geometric Deep Learning
In this first in a series of posts on group-equivariant convolutional neural networks (GCNNs), meet the main actors — groups — and concepts (equivariance). With GCNNs, we finally revisit the topic of Geometric Deep Learning, a principled, math-driven approach to neural networks that has consistently been rising in scope and impact.

AO, NAO, ENSO: A wavelet analysis example
El Niño-Southern Oscillation (ENSO), North Atlantic Oscillation (NAO), and Arctic Oscillation (AO) are atmospheric phenomena of global impact that strongly affect people's lives. ENSO, first and foremost, brings with it floods, droughts, and ensuing poverty, in developing countries in the Southern Hemisphere. Here, we use the new torchwavelets package to comparatively inspect patterns in the three series.

Discrete Fourier Transform - with torch
About the Fourier Transform, it has been said that it is one of the greatest wonders of the universe. At the same time, it can be realized in a mere half-dozen lines of code. Even if in the end, you're just going to call torch's built-in functions directly, it helps to understand, and be able to reproduce in code, the ideas that underlie the magic. This post is an excerpt from the forthcoming book, Deep Learning and Scientific Computing with R torch, to be published by CRC Press.

Five ways to do least squares (with torch)
Get to know torch's linalg module, all while learning about different ways to do least-squares regression from scratch. This post is a condensed version of the corresponding chapter in the forthcoming book, Deep Learning and Scientific Computing with R torch, to be published by CRC Press.

Audio classification with torch
Learn how to classify speech utterances with torch, making use of domain knowledge and deep learning. This post is a condensed version of the corresponding chapter in the forthcoming book, Deep Learning and Scientific Computing with R torch, to be published by CRC Press.

Deep Learning with R, 2nd Edition
Announcing the release of "Deep Learning with R, 2nd Edition," a book that shows you how to get started with deep learning in R.

Starting to think about AI Fairness
The topic of AI fairness metrics is as important to society as it is confusing. Confusing it is due to a number of reasons: terminological proliferation, abundance of formulae, and last not least the impression that everyone else seems to know what they're talking about. This text hopes to counteract some of that confusion by starting from a common-sense approach of contrasting two basic positions: On the one hand, the assumption that dataset features may be taken as reflecting the underlying concepts ML practitioners are interested in; on the other, that there inevitably is a gap between concept and measurement, a gap that may be bigger or smaller depending on what is being measured. In contrasting these fundamental views, we bring together concepts from ML, legal science, and political philosophy.

Beyond alchemy: A first look at geometric deep learning
Geometric deep learning is a "program" that aspires to situate deep learning architectures and techniques in a framework of mathematical priors. The priors, such as various types of invariance, first arise in some physical domain. A neural network that well matches the domain will preserve as many invariances as possible. In this post, we present a very conceptual, high-level overview, and highlight a few applications.

Introductory time-series forecasting with torch
This post is an introduction to time-series forecasting with torch. Central topics are data input, and practical usage of RNNs (GRUs/LSTMs). Upcoming posts will build on this, and introduce increasingly involved architectures.

Forecasting El Niño-Southern Oscillation (ENSO)
El Niño-Southern Oscillation (ENSO) is an atmospheric phenomenon, located in the tropical Pacific, that greatly affects ecosystems as well as human well-being on a large portion of the globe. We use the convLSTM introduced in a prior post to predict the Niño 3.4 Index from spatially-ordered sequences of sea surface temperatures.

torch, tidymodels, and high-energy physics
Today we introduce tabnet, a torch implementation of "TabNet: Attentive Interpretable Tabular Learning" that is fully integrated with the tidymodels framework. Per se, already, tabnet was designed to require very little data pre-processing; thanks to tidymodels, hyperparameter tuning (so often cumbersome in deep learning) becomes convenient and even, fun!

Convolutional LSTM for spatial forecasting
In forecasting spatially-determined phenomena (the weather, say, or the next frame in a movie), we want to model temporal evolution, ideally using recurrence relations. At the same time, we'd like to efficiently extract spatial features, something that is normally done with convolutional filters. Ideally then, we'd have at our disposal an architecture that is both recurrent and convolutional. In this post, we build a convolutional LSTM with torch.
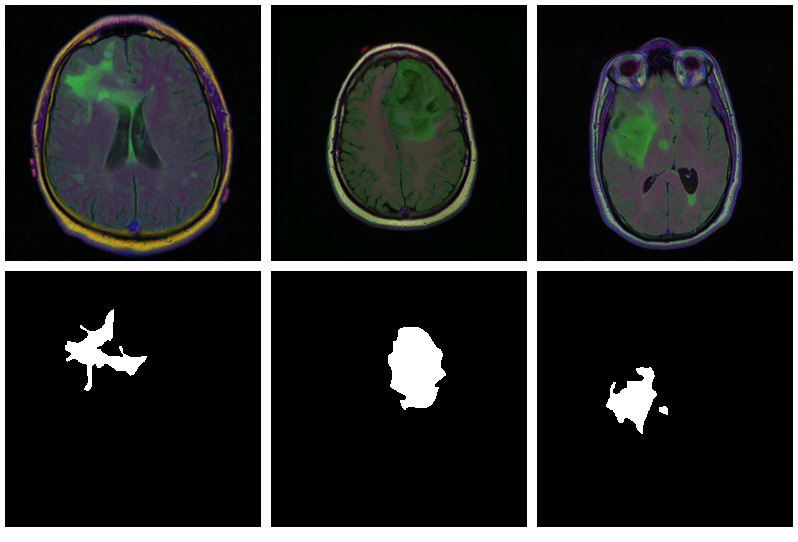
Brain image segmentation with torch
The need to segment images arises in various sciences and their applications, many of which are vital to human (and animal) life. In this introductory post, we train a U-Net to mark lesioned regions on MRI brain scans.

FNN-VAE for noisy time series forecasting
In the last part of this mini-series on forecasting with false nearest neighbors (FNN) loss, we replace the LSTM autoencoder from the previous post by a convolutional VAE, resulting in equivalent prediction performance but significantly lower training time. In addition, we find that FNN regularization is of great help when an underlying deterministic process is obscured by substantial noise.

Time series prediction with FNN-LSTM
In a recent post, we showed how an LSTM autoencoder, regularized by false nearest neighbors (FNN) loss, can be used to reconstruct the attractor of a nonlinear, chaotic dynamical system. Here, we explore how that same technique assists in prediction. Matched up with a comparable, capacity-wise, "vanilla LSTM", FNN-LSTM improves performance on a set of very different, real-world datasets, especially for the initial steps in a multi-step forecast.
Deep attractors: Where deep learning meets chaos
In nonlinear dynamics, when the state space is thought to be multidimensional but all we have for data is just a univariate time series, one may attempt to reconstruct the true space via delay coordinate embeddings. However, it is not clear a priori how to choose dimensionality and time lag of the reconstruction space. In this post, we show how to use an autoencoder architecture to circumvent the problem: Given just a scalar series of observations, the autoencoder directly learns to represent attractors of chaotic systems in adequate dimensionality.

Hacking deep learning: model inversion attack by example
Compared to other applications, deep learning models might not seem too likely as victims of privacy attacks. However, methods exist to determine whether an entity was used in the training set (an adversarial attack called member inference), and techniques subsumed under "model inversion" allow to reconstruct raw data input given just model output (and sometimes, context information). This post shows an end-to-end example of model inversion, and explores mitigation strategies using TensorFlow Privacy.

Infinite surprise - the iridescent personality of Kullback-Leibler divergence
Kullback-Leibler divergence is not just used to train variational autoencoders or Bayesian networks (and not just a hard-to-pronounce thing). It is a fundamental concept in information theory, put to use in a vast range of applications. Most interestingly, it's not always about constraint, regularization or compression. Quite on the contrary, sometimes it is about novelty, discovery and surprise.